Note
Go to the end to download the full example code.
Averaging order#
This example compares two different workflows that accomplish the same task to show how the order of the operators can change the end result.
The first workflow extracts the stress field of a crankshaft under load from a result file, computes the equivalent (von Mises) stresses, and then applies an averaging operator to transpose them from
ElementalNodaltoNodalpositions.The second workflow first transposes the stresses that come from the result file to a
Nodalposition and then calculates the von Mises stresses.
The following images shows these workflows:
![digraph foo {
graph [pad="0", nodesep="0.3", ranksep="0.3"]
node [shape=box, style=filled, fillcolor="#ffcc0", margin="0"];
rankdir=LR;
splines=line;
node [fixedsize=true,width=2.5]
stress01 [label="stress"];
stress02 [label="stress"];
vm01 [label="von_mises_eqv"];
vm02 [label="von_mises_eqv"];
avg01 [label="elemental_nodal_to_nodal", width=2.5];
avg02 [label="elemental_nodal_to_nodal", width=2.5];
subgraph cluster_1 {
ds01 [label="data_src", shape=box, style=filled, fillcolor=cadetblue2];
ds01 -> stress01 [style=dashed];
stress01 -> vm01;
vm01 -> avg01
label="Compute Von Mises then average stresses";
style=filled;
fillcolor=lightgrey;
}
subgraph cluster_2 {
ds02 [label="data_src", shape=box, style=filled, fillcolor=cadetblue2];
ds02 -> stress02 [style=dashed];
stress02 -> avg02;
avg02 -> vm02
label="Average stresses then compute Von Mises";
style=filled;
fillcolor=lightgrey;
}
}](../../_images/graphviz-91f1b48e5b64f3c16fab7b9f92f4be128a5e5611.png)
Import the necessary modules.
from ansys.dpf import core as dpf
from ansys.dpf.core import examples
Load the simulation results from an RST file.
analysis = examples.download_crankshaft()
Create the first workflow#
The first workflow applies the averaging operator after computing the equivalent stresses. To create it, define a function that computes the von Mises stresses in the crankshaft and then apply the averaging operator.
def compute_von_mises_then_average(analysis):
# Create a model from the results of the simulation and retrieve its mesh
model = dpf.Model(analysis)
# Apply the stress operator to obtain the stresses in the body
stress_op = dpf.operators.result.stress()
stress_op.inputs.connect(model)
stresses = stress_op.outputs.fields_container()
# Compute the von Mises stresses
vm_op = dpf.operators.invariant.von_mises_eqv()
vm_op.inputs.field.connect(stresses)
von_mises = vm_op.outputs.field()
# Apply the averaging operator to the von Mises stresses
avg_op = dpf.operators.averaging.elemental_nodal_to_nodal()
avg_op.inputs.connect(von_mises)
avg_von_mises = avg_op.outputs.field()
# Find the maximum value of the von Mises stress field
min_max = dpf.operators.min_max.min_max()
min_max.inputs.field.connect(avg_von_mises)
max_val = min_max.outputs.field_max()
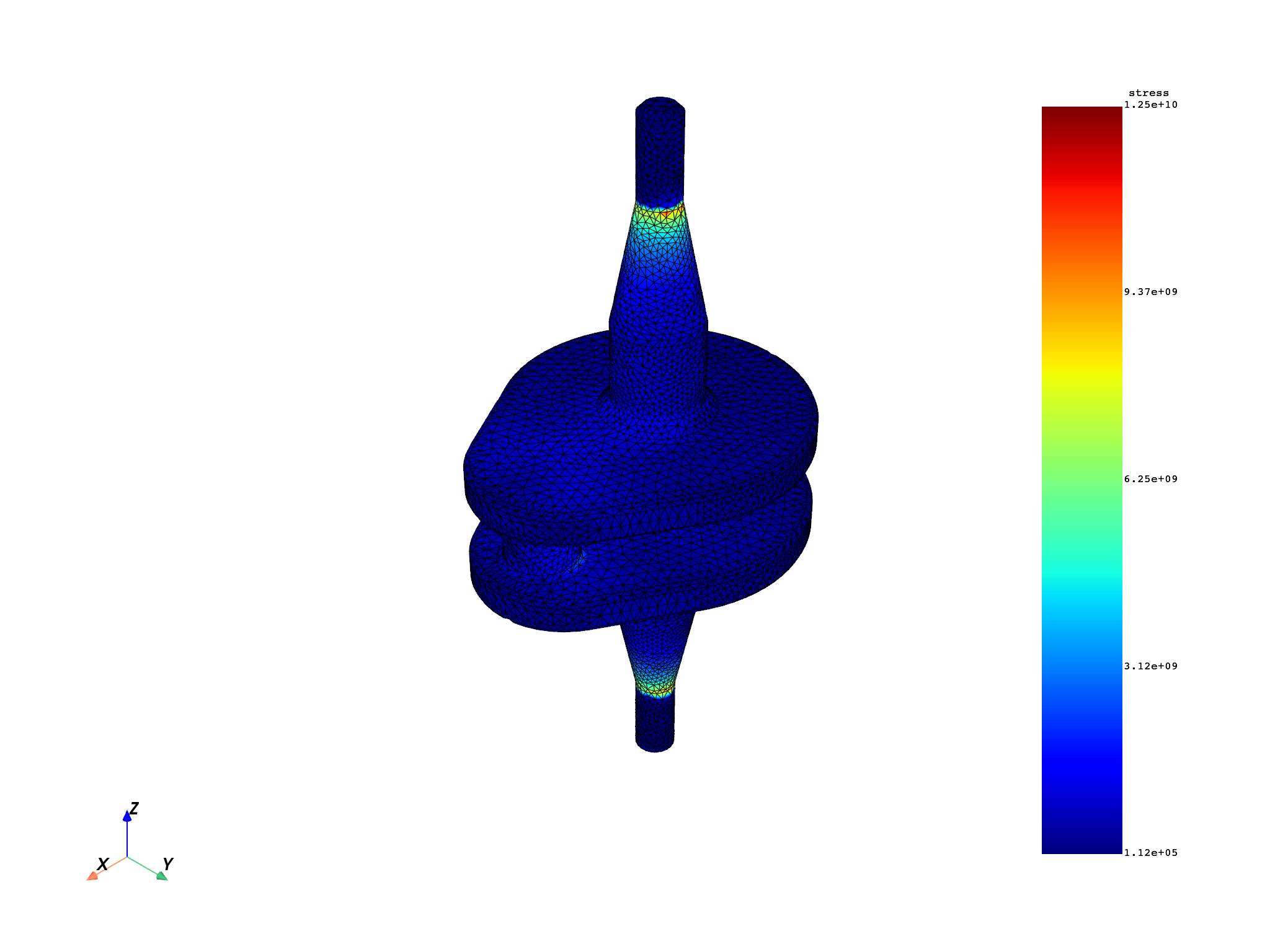
avg_von_mises.plot()
return max_val.data[0]
Create the second workflow#
The second workflow computes the equivalent stresses after applying the averaging
operator. To create this workflow, first apply the averaging operator to the
stress field in the crankshaft and then calculate the von Mises stresses, which
are already located on a Nodal position.
def average_then_compute_von_mises(analysis):
# Creating the model from the results of the simulation
model = dpf.Model(analysis)
# Retrieving the stresses
stress_op = dpf.operators.result.stress()
stress_op.inputs.connect(model)
stresses = stress_op.outputs.fields_container()
# Averaging the stresses to a Nodal position
avg_op = dpf.operators.averaging.elemental_nodal_to_nodal()
avg_op.inputs.connect(stresses)
avg_stresses = avg_op.outputs.field()
# Computing the Von Mises stresses
vm_op = dpf.operators.invariant.von_mises_eqv()
vm_op.inputs.field.connect(avg_stresses)
avg_von_mises = vm_op.outputs.field()
# Finding the maximum Von Mises stress value
min_max = dpf.operators.min_max.min_max()
min_max.inputs.field.connect(avg_von_mises)
max_val = min_max.outputs.field_max()
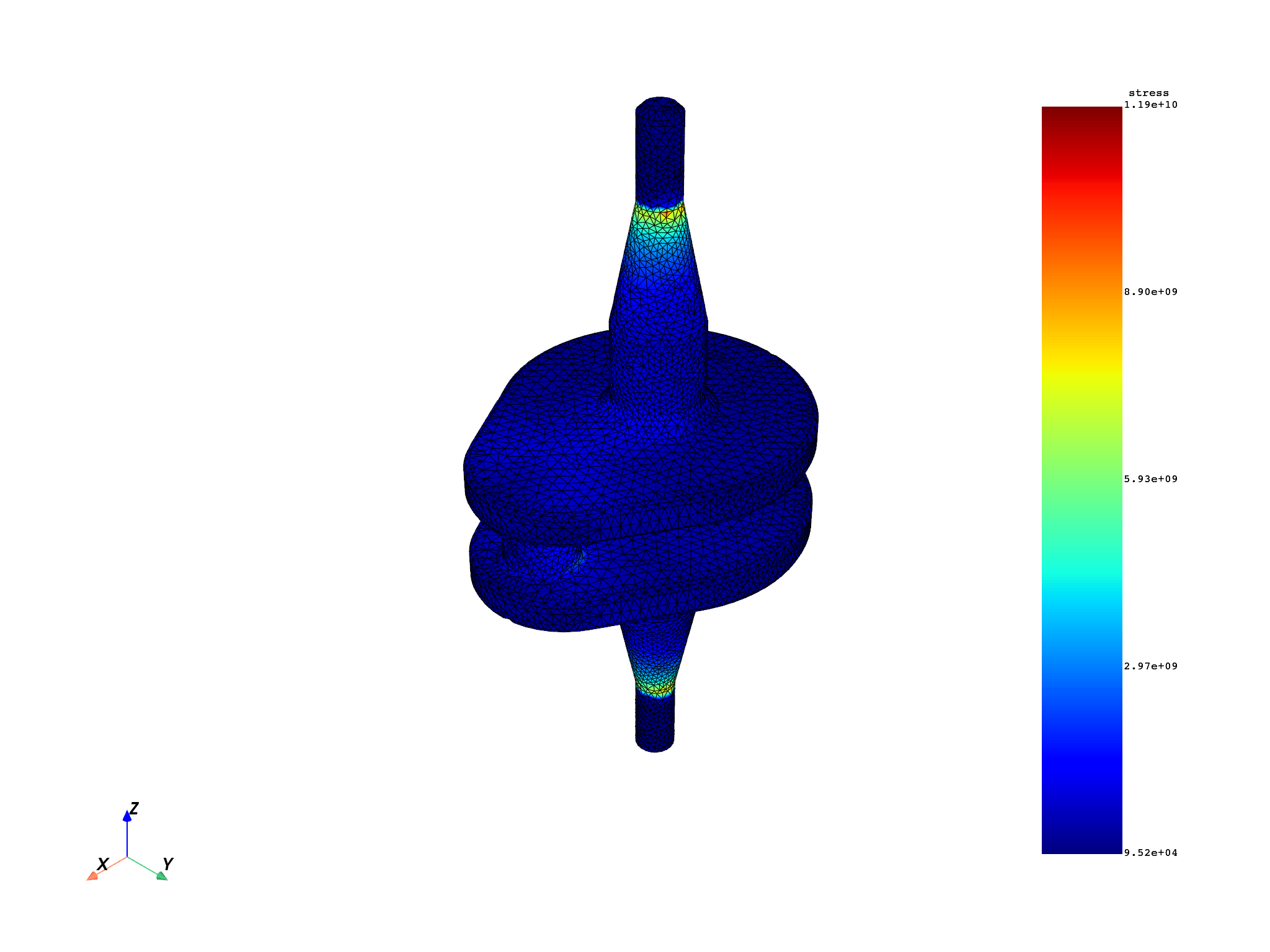
avg_von_mises.plot()
return max_val.data[0]
Plot the results#
Plot both von Mises stress fields side by side to compare them. - The first plot displays the results when the equivalent stresses are calculated first. - The second plot shows the results when the averaging is done first.
max1 = compute_von_mises_then_average(analysis)
max2 = average_then_compute_von_mises(analysis)
diff = (max1 - max2) / max2 * 100
print("Max stress when Von Mises is computed first: {:.2f} Pa".format(max1))
print("Max stress when the stress averaging is done first: {:.2f} Pa".format(max2))
print(
"The maximum Von Mises stress value is {:.2f}% higher when \
the averaging is done after the calculations.".format(diff)
)
Max stress when Von Mises is computed first: 12494955907.48 Pa
Max stress when the stress averaging is done first: 11860260659.06 Pa
The maximum Von Mises stress value is 5.35% higher when the averaging is done after the calculations.
Even though both workflows apply the same steps to the same initial data, their final results are different because of the order in which the operators are applied.
Total running time of the script: (0 minutes 6.352 seconds)